The image of an object placed at

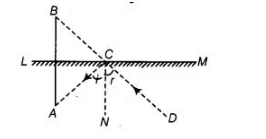
Given An object $O A$ placed at a point $A, L M$ be a plane mirror, $D$ be an observer and $O B$ is the image.

To prove The image is as far behind the mirror as the object is in front of the mirror i.e., $O B=O A$

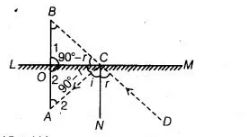
Proof $\because C N \perp L M$ and $A B \perp L M$

$\Rightarrow \quad A B \| C N$

$\angle A=\angle i$ [alternate interior angles] ...(i)

$\angle B=\angle r \quad$ [corresponding angles] ...(ii)

Also, $\angle i=\angle r$ $[\because$ incident angle $=$ reflected angle $] \ldots$ (iii)

From Eqs. (i), (ii) and (iii), $\angle A=\angle B$

In $\Delta C O B$ and $\triangle C O A$, $\angle B=\angle A$ [proved above]

$\angle 1=\angle 2$ [each 90°]

and $C O=C O$ [common side]

$\therefore$ $\Delta C O B \cong \Delta C O A$ [by AAS congruence rule]

$\Rightarrow$ $O B=O A$ [by CPCT]

Hence proved.

Alternate Method

In $\triangle O B C$ and $\triangle O A C$, $\angle 1=\angle 2$ [each 90°]

Also, $\angle i=\angle r$ $[\because$ incident angle $=$ reflected angle $] \ldots(1)$

On multiplying both sides of Eq. (1) by $-1$ and then adding $90^{\circ}$ both sides, we get

$90^{\circ}-\angle i=90^{\circ}-\angle r$

$\Rightarrow$ $\angle A C O=\angle B C O$ 

and  $O C=O C$ [common side]

$\therefore$ $\triangle O B C \cong \triangle O A C$ [by ASA congruence rule]

$\Rightarrow$ $B=O A$ [by CPCT]

Hence, the image is as far behind the mirror as the object is in front of the mirror.