The height of a tower is 100 m. When the angle of elevation of the sun

The given situation can be represented as,

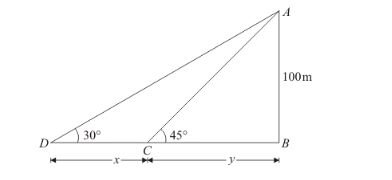
Here, AB is the tower of height  meters.

When angle of elevation of sun changes from $\angle D=30^{\circ}$ to $\angle C=45^{\circ}, C D=x$.

We assumed that $B C=y$

Here we have to find the value of $x$

So we use trigonometric ratios.

In a triangle,

$\Rightarrow \tan C=\frac{A B}{B C}$

$\Rightarrow \tan 45^{\prime}=\frac{A B}{B C}$

$\Rightarrow \mathrm{I}=\frac{100}{y}$

$\Rightarrow y=100$

Again in a triangle ABD,

$\Rightarrow \tan D=\frac{A B}{B C+C D}$

$\Rightarrow \tan 30^{\circ}=\frac{100}{x+y}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{100}{x+y}$

$\Rightarrow 100 \sqrt{3}=x+y$

$\Rightarrow 100 \sqrt{3}=x+100$

$\Rightarrow x=100(\sqrt{3}-1)^{\mathrm{P}}$   Put $x=100$

Hence the correct option is c.