Question:
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm, and height 4 cm are cut off. Find the volume of the remaining solid.
Solution:
Volume of cylinder
$=\pi r^{2} h$
$=\pi \times\left(\frac{7}{2}\right)^{2} \times 15$
$=\frac{735}{4} \pi \mathrm{cm}^{3}$
$=183.75 \pi \mathrm{cm}^{2}$
Volume of cones
$=2 \times\left(\frac{1}{3} \pi r^{2} h\right)$
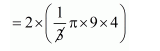
$=24 \pi \mathrm{cm}^{3}$
Volume of remaining solid
$=183.75 \pi-24 \pi$
$=502.1 \mathrm{~cm}^{3}$
