Question:
The graphs of sine and cosine functions, intersect each other at a number of points and between two consecutive points of intersection, the two graphs enclose the same area $A$. Then $A^{4}$ is equal to
Solution:
$
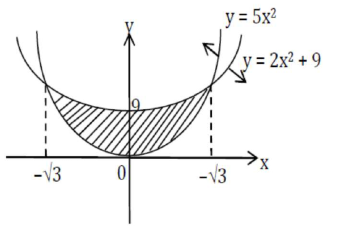
Required area
$=2 \int_{0}^{\sqrt{3}}\left(2 x^{2}+9-5 x^{2}\right) d x$
$=2 \int_{0}^{\sqrt{3}}\left(9-3 x^{2}\right) d x$
$=2\left|9 x-x^{3}\right|_{0}^{\sqrt{3}}=12 \sqrt{3}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.