The given figure shows a pentagon ABCDE. EG, drawn parallel to DA, meets BA produced at G, and CF, drawn parallel to DB, meets AB produced at F.

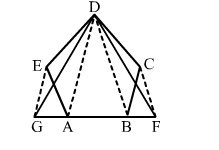
Given:  ABCDE is a pentagon.  EG || DA and CF || DB.
To prove: ar(pentagon ABCDE ) =  ar( ∆DGF) 
Proof: 
ar(pentagon ABCDE )​ = ar(∆DBC) + ar(∆ADE ) + ar(∆ABD)               ...(i)
Also, ar(∆DGF) = ar(∆DBF) + ar(∆ADG) + ar(∆ABD )                ...(ii)

Now, ∆DBC and ∆DBF lie on the same base and between the same parallel lines. 
∴ ar(∆DBC) = ar(∆DBF)                         ...(iii)               
Similarly, ∆ADE and ∆ADG lie on same base and between the same parallel lines.  
 ∴ ar(∆ADE) = ar(∆ADG)                       ...(iv)

From (iii) and (iv), we have:
ar(∆DBC) + ar(∆ADE) = ar(∆DBF) + ar(∆ADG)
Adding ar(∆ABD) on both sides, we get:
ar(∆DBC) + ar(∆ADE) + ar(∆ABD) = ar (∆DBF) + ar(∆ADG) + ar(∆ABD) 
By substituting the values from (i) and (ii), we get:
ar(pentagon ABCDE) =  ar(∆DGF)