Question:
The function $f: R \rightarrow R$ defined by $f(x)=6^{x}+6^{|x|}$ is
(a) one-one and onto
(b) many one and onto
(c) one-one and into
(d) many one and into
Solution:
(d) many one and into
Graph of the given function is as follows :
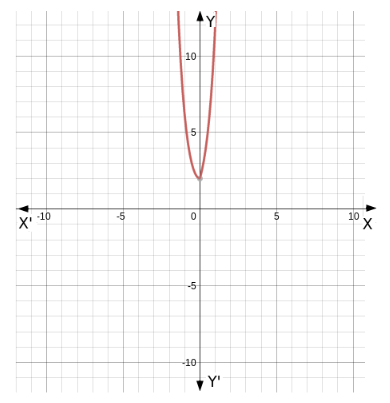
A line parallel to X axis is cutting the graph at two different values.
Therefore, for two different values of x we are getting the same value of y .
That means it is many one function .
From the given graph we can see that the range is $[2, \infty)$ and $R$ is the codomain of the given function.
Hence, Codomain $\neq$ Range
Therefore, the given function is into.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.