The function $f(x)=x^{3}-6 x^{2}+a x+b$ is such that $f(2)=f(4)=0 .$ Consider two statements.
$(\mathrm{S} 1)$ there exists $\mathrm{x}_{1}, \mathrm{x}_{2} \in(2,4), \mathrm{x}_{1}<\mathrm{x}_{2}$, such that $f^{\prime}\left(x_{1}\right)=-1$ and $f^{\prime}\left(x_{2}\right)=0 .$
$(\mathrm{S} 2)$ there exists $\mathrm{x}_{3}, \mathrm{x}_{4} \in(2,4), \mathrm{x}_{3}<\mathrm{x}_{4}$, such that
$f$ is decreasing in $\left(2, x_{4}\right)$, increasing in $\left(x_{4}, 4\right)$
and $2 f^{\prime}\left(\mathrm{x}_{3}\right)=\sqrt{3} f\left(\mathrm{x}_{4}\right)$.
Then
Correct Option: 1
$f(x)=x^{3}-6 x^{2}+a x+b$
$f(2)=8-24+2 a+b=0$
$2 a+b=16 \ldots(1)$...(1)
$f(4)=64-96+4 a+b=0$
$4 a+b=32 \ldots(2)$...(2)
Solving (1) and (2)
$a=8, b=0$
$f(x)=x^{3}-6 x^{2}+8 x$
$f(x)=x^{3}-6 x^{2}+8 x$
$f^{\prime}(x)=3 x^{2}-12 x+8$
$f^{\prime \prime}(x)=6 x-12$
$\Rightarrow \mathrm{f}^{\prime}(\mathrm{x})$ is $\uparrow$ for $\mathrm{x}>2$, and $\mathrm{f}^{\prime}(\mathrm{x})$ is $\downarrow$ for $\mathrm{x}<2$
$f^{\prime}(2)=12-24+8=-4$
$f^{\prime}(4)=48-48+8=8$
$f^{\prime}(x)=3 x^{2}-12 x+8$
vertex $(2,-4)$
$f^{\prime}(2)=-4, f^{\prime}(4)=8, f^{\prime}(3)=27-36+8$
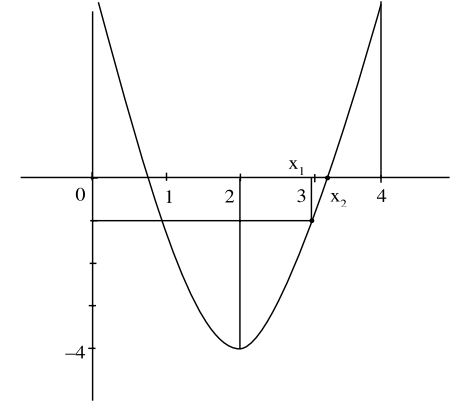
$f^{\prime}\left(x_{1}\right)=-1$, then $x_{1}=3$
$f^{\prime}\left(x_{2}\right)=0$
Again
$f^{\prime}(x)<0$ for $x \in\left(2, x_{4}\right)$
$\mathrm{f}^{\prime}(\mathrm{x})>0$ for $\mathrm{x} \in\left(\mathrm{x}_{4}, 4\right)$
$x_{4} \in(3,4)$
$f(x)=x^{3}-6 x^{2}+8 x$
$f(3)=27-54+24=-3$
$f(4)=64-96+32=0$
For $x_{4}(3,4)$
$f\left(x_{4}\right)<-3 \sqrt{3}$
and $f^{\prime}\left(x_{3}\right)>-4$
$2 \mathrm{f}^{\prime}\left(\mathrm{x}_{3}\right)>-8$
So, $2 \mathrm{f}^{\prime}\left(\mathrm{x}_{2}\right)=\sqrt{3} \mathrm{f}\left(\mathrm{x}_{4}\right)$
Correct Ans. (1)
