The front compound wall of a house is decorated by wooden spheres of diameter $21 \mathrm{~cm}$, placed on small supports as shown in the figure. Eight such spheres are used for this purpose and are to be painted silver. Each support is a cylinder of radius $1.5 \mathrm{~cm}$ and height $7 \mathrm{~cm}$ and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per $\mathrm{cm}^{2}$.
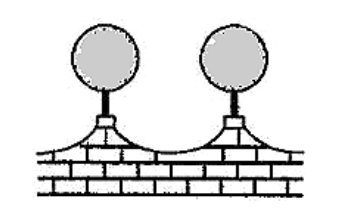
Wooden sphere radius = 21/2 = 10.5 cm
Surface area of a wooden sphere $=4 \pi r^{2}=4 \times 22 / 7 \times(10.5)^{2}=1386 \mathrm{~cm}^{2}$
Radius r of cylindrical support = 1.5 cm
Height h of cylindrical support = 7cm
Curved surface area of cylindrical support $=2 \pi r h=2 \times 22 / 7 \times 1.5 \times 7=66 \mathrm{~cm}^{2}$
Area of circular end of cylindrical support $=\pi r^{2}=22 / 7 \times(1.5)^{2}=7.07 \mathrm{~cm}^{2}$
Area to be painted silver $=8(1386-7.07) \mathrm{cm}^{2}$
$=8(1378.93) \mathrm{cm}^{2}$
$=11031.44 \mathrm{~cm}^{2}$
Cost occurred in painting silver colour = (11034.44 × 0.25) = Rs.2757.86
Area to be painted black $=(8 \times 66) \mathrm{cm}^{2}=528 \mathrm{~cm}^{2}$
Cost occurred in painting black colour = (528 × 5.05) = Rs.26.40
Therefore total cost in painting = Rs.2757.86 + Rs.26.40
= Rs.2784.26
