The frequency of a car horn encountered a change from $400 \mathrm{~Hz}$ to $500 \mathrm{~Hz}$. When the car approaches a vertical wall. If the speed of sound is $330 \mathrm{~m} / \mathrm{s}$. Then the speed of car is_________ $\mathrm{km} / \mathrm{h}$.
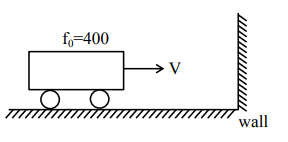
Wall as an observer
Frequency received by wall
$\mathrm{f}_{1}=\mathrm{f}_{0}\left(\frac{\mathrm{C}}{\mathrm{C}-\mathrm{V}}\right)$
Again wall as a source
Frequency received by observer on car
$f_{2}=f_{1}\left(\frac{C+V}{C}\right)$
$f_{2}=f_{0}\left(\frac{C+V}{C-V}\right)$
$500=400\left(\frac{\mathrm{C}+\mathrm{V}}{\mathrm{C}-\mathrm{V}}\right)$
$\frac{5}{4}=\frac{C+V}{C-V}$
$C=9 V$
$\mathrm{V}=\frac{\mathrm{C}}{9}=\frac{330}{9} \mathrm{~m} / \mathrm{s}$
$\mathrm{V}=\frac{330}{9} \times \frac{18}{5}=132 \mathrm{~km} / \mathrm{hr}$
