Question:
The four arms of a Wheatstone bridge have resistances as shown in the figure. A galvanometer of $15 \Omega$ resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of $10 \mathrm{~V}$ is maintained across $\mathrm{AC}$.
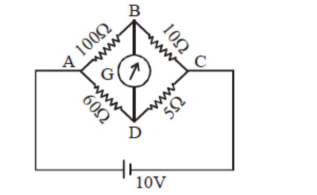
Correct Option: , 3
Solution:
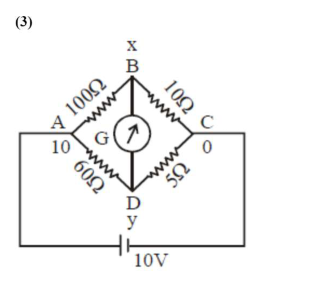
$\frac{x-10}{100}+\frac{x-y}{15}+\frac{x-0}{10}=0$
$53 x-20 y=30 \ldots . .(1)$
$\frac{y-10}{60}+\frac{y-x}{15}+\frac{y-0}{5}=0$
$17 y-4 x=10 \ldots \ldots(2)$
on solving (1)\&(2)
$\mathrm{x}=0.865$
$\mathrm{y}=0.792$
$\Delta \mathrm{V}=0.073 \mathrm{R}=15 \Omega$
$\mathrm{i}=4.87 \mathrm{~mA}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.