The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D
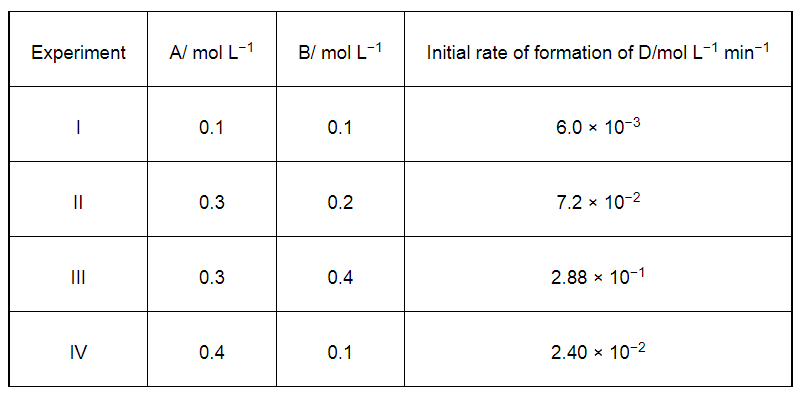
Determine the rate law and the rate constant for the reaction.
Let the order of the reaction with respect to A be x and with respect to B be y.
Therefore, rate of the reaction is given by,
Rate $=k[\mathrm{~A}]^{x}[\mathrm{~B}]^{y}$
According to the question,
$6.0 \times 10^{-3}=k[0.1]^{x}[0.1]^{y}$ ...(i)
$7.2 \times 10^{-2}=k[0.3]^{x}[0.2]^{y}$ ...(ii)
$2.88 \times 10^{-1}=k[0.3]^{x}[0.4]^{y}$ ...(iii)
$2.40 \times 10^{-2}=k[0.4]^{x}[0.1]^{y}$ ...(iv)
Dividing equation (iv) by (i), we obtain
$\frac{2.40 \times 10^{-2}}{6.0 \times 10^{-3}}=\frac{k[0.4]^{x}[0.1]^{y}}{k[0.1]^{x}[0.1]^{y}}$
$\Rightarrow 4=\frac{[0.4]^{x}}{[0.1]^{x}}$
$\Rightarrow 4=\left(\frac{0.4}{0.1}\right)^{x}$
$\Rightarrow(4)^{1}=4^{x}$
$\Rightarrow x=1$
Dividing equation (iii) by (ii), we obtain
$\frac{2.88 \times 10^{-1}}{7.2 \times 10^{-2}}=\frac{k[0.3]^{x}[0.4]^{y}}{k[0.3]^{x}[0.2]^{y}}$
$\Rightarrow 4=\left(\frac{0.4}{0.2}\right)^{y}$
$\Rightarrow 4=2^{y}$
$\Rightarrow 2^{2}=2^{y}$
$\Rightarrow 4=2^{y}$
$\Rightarrow 2^{2}=2^{y}$
$\Rightarrow y=2$
Therefore, the rate law is
Rate = k [A] [B]2
$\Rightarrow k=\frac{\text { Rate }}{[\mathrm{A}][\mathrm{B}]^{2}}$
From experiment I, we obtain
$k=\frac{6.0 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{\left(0.1 \mathrm{~mol} \mathrm{~L}^{-1}\right)\left(0.1 \mathrm{~mol} \mathrm{~L}^{-1}\right)^{2}}$
= 6.0 L2 mol−2 min−1
From experiment II, we obtain
$k=\frac{7.2 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{\left(0.3 \mathrm{~mol} \mathrm{~L}^{-1}\right)\left(0.2 \mathrm{~mol} \mathrm{~L}^{-1}\right)^{2}}$
= 6.0 L2 mol−2 min−1
From experiment III, we obtain
$k=\frac{2.88 \times 10^{-1} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{\left(0.3 \mathrm{~mol} \mathrm{~L}^{-1}\right)\left(0.4 \mathrm{~mol} \mathrm{~L}^{-1}\right)^{2}}$
= 6.0 L2 mol−2 min−1
From experiment IV, we obtain
$k=\frac{2.40 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{\left(0.4 \mathrm{~mol} \mathrm{~L}^{-1}\right)\left(0.1 \mathrm{~mol} \mathrm{~L}^{-1}\right)^{2}}$
= 6.0 L2 mol−2 min−1
Therefore, rate constant, k = 6.0 L2 mol−2 min−1
