Question:
The following is the distribution of height of students of a certain class in a certain city:
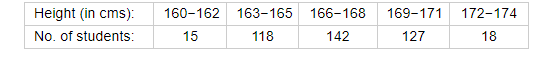
Find the median height.
Solution:
First we prepare the following cummulative table to compute the median.
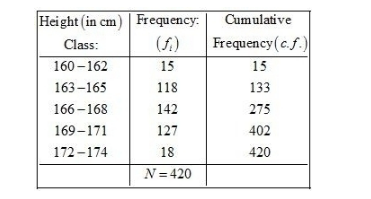
Now, $N=420$
$\therefore \frac{N}{2}=210$
Thus, the cumulative frequency just greater than 210 is 275 and the corresponding class is $166-168$.
Therefore, $166-168$ is the median class.
$I=166, f=142, F=133$ and $h=2$
We know that,
Median $=l+\left\{\frac{\frac{N}{2}-F}{f}\right\} \times h$
$=166+\left\{\frac{210-133}{142}\right\} \times 2$
$=166+\frac{77 \times 2}{142}$
$=166+\frac{154}{142}$
$=166+1.08$
$=167.08$
Hence, the median height is approximately 167.1 cm.
