Question:
The figure shows a square loop $\mathrm{L}$ of side $5 \mathrm{~cm}$ which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of $1 \mathrm{~cm} \mathrm{~s}^{-1}$. At some instant, a part of $\mathrm{L}$ is in a uniform magnetic field of 1 $\mathrm{T}$, perpendicular to the plane of the loop. If the resistance of $\mathrm{L}$ is $1.7 \Omega$, the current in the loop at that instant will be close to :
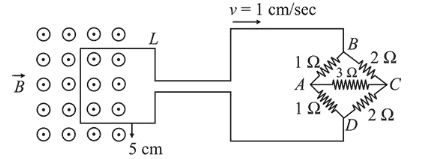
Correct Option: , 2
Solution:
(2) Induced emf,
$e=B v \ell=1 \times 10^{-2} \times 0.05=5 \times 10^{-4} \mathrm{~V}$
Equivalent resistance,
$R=\frac{4 \times 2}{4+2}+1.7$
$=\frac{4}{3}+1.7 \simeq 3 \Omega$
Current, $i=\frac{e}{R}=\frac{5 \times 10^{-4}}{3} \simeq 170 \mu \mathrm{A}$
