The figure obtained by joining the mid-points

(d)

Here, length of rectangle ABCD = 8 cm and breadth of rectangle ABCD = 6.cm

Let E, F, G and H are the mid-points of the sides of rectangle ABCD, then EFGH is a rhombus.

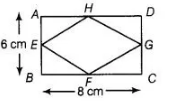
Here, $\quad$ length of rectangle $A B C D=8 \mathrm{~cm}$

and breadth of rectangle $A B C D=6, \mathrm{~cm}$

Let $E, F, G$ and $H$ are the mid-points of the sides of rectangle $A B C D$, then $E F G H$ is a rhombus.

Then, diagonal of rhombus $E F G H$ are $E G$ and $H F$.

Here, $E G=B C=8 \mathrm{~cm}$

and $H F=A B=6 \mathrm{~cm}$

$\therefore$Area of rhombus $=\frac{\text { Product of diagonals }}{2}$

$=\frac{8 \times 6}{2}=4 \times 6=24 \mathrm{~cm}^{2}$

Hence, joining the mid-points of the adjacent sides of a rectangle forms a thombus of area $24 \mathrm{~cm}^{2}$.