The figure obtained by joining the

(b) Let $A B C D$ be a rhombus in which $P, Q, R$ and $S$ are the mid-points of sides $A B, B C, C D$ and $D A$, respectively.

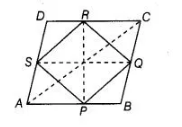
Join $A C, P R$ and $S Q$

In $\triangle A B C, P$ is the mid-point of $A B$ and $Q$ is the mid-point of $B C$.

$\Rightarrow \quad P Q \| A C$ and $P Q=\frac{1}{2} A C \quad[$ by using mid-point theorem] ...(i)

Similarly, in $\triangle D A C$,

$S R \| A C$ and $S R=\frac{1}{2} A C$ ...(ii)

From Eqs. (i) and (ii),

$P Q^{\prime} \| S R$ and $P Q=S R$

So, $P Q R S$ is a parallelogram.

Also, $A B Q S$ is a parallelogram.

$\Rightarrow \quad A B=S Q$ .....(iii)

[opposite sides of a parallelogram are equal]

Similarly, $P B C R$ is a parallelogram.

$B C=P R$ [opposite sides of a parallelogram are equal]

$\Rightarrow \quad A B=P R \quad[\because B C=A B$ sides of a rhombus $]$

$\Rightarrow \quad S Q=P R \quad$ [from Eq. (iii)]

So, the diagonals of a parallelogram are equal. Hence, PQRS is a rectangle.