The figure formed by joining the

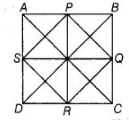
(c) Given, $A B C D$ is a quadrilateral and $P, Q, R$ and $S$ are the mid-points of sides of $A B, B C$, $C D$ and $D A$, respectively. Then, $P Q R S$

is a square.

$\therefore \quad P Q=Q R=R S=P S \quad$ .......(i)

and $P R=S Q$

But $P R=B C$ and $S Q=A B$

$\therefore \quad A B=B C$

Thus, all the sides of quadrilateral $A B C D$ are equal.

Hence, quadrilateral $A B C D$ is either a square or a rhombus.

Now, in $\triangle A D B$, use mid-point theorem

$S P \| D B$

and $S P=\frac{1}{2} D B$ ... (ii)

Similarly in $\triangle A B C$ (by mid-point theorem) $P Q \| A C$ and $P Q=\frac{1}{2} A C$ ... (iii)

From Eq. (i), $P S=P Q$

$\Rightarrow$ $\frac{1}{2} D B=\frac{1}{2} A C$ [from Eqs. (ii) and (iii)]

$\Rightarrow \quad D B=A C$

Thus, diagonals of $A B C D$ are equal and therefore quadrilateral $A B C D$ is a square not rhombus. So, diagonals of quadrilateral are also perpendicular.