The equilibrium constant $K_{c}$ at $298 K$ for the reaction $\mathrm{A}+\mathrm{B} \rightleftharpoons \mathrm{C}+\mathrm{D}$
is 100 . Starting with an equimolar solution with concentrations of $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$ all equal to $1 \mathrm{M}$, the equilibrium concentration of $\mathrm{D}$ is $\times 10^{-2}$
M. (Nearest integer)
$\mathrm{A}+\mathrm{B} \rightleftharpoons \mathrm{C}+\mathrm{D}: \mathrm{K}_{\mathrm{eq}}=100$
$1 \mathrm{M} \quad 1 \mathrm{M} \quad 1 \mathrm{M} \quad 1 \mathrm{M}$
First check direction of reversible reaction.
Since $\mathrm{Q}_{\mathrm{C}}=\frac{[\mathrm{C}][\mathrm{D}]}{[\mathrm{A}][\mathrm{B}]}=1<\mathrm{K}_{\text {eq. }} \Rightarrow$ reaction will move in forward direction to attain equilibrium state.
$\Rightarrow \mathrm{A}+\mathrm{B} \rightleftharpoons \mathrm{C}+\mathrm{D}: \mathrm{K}_{\mathrm{eq}}=100$
to $1 \quad 1 \quad 1 \quad 1$
Now $: K_{e q}=100=\frac{(1+x)(1+x)}{(1-x)(1-x)}$
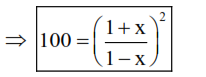
(i) $10=\left(\frac{1+x}{1-x}\right)$
$\Rightarrow 10-10 x=1+x$
$\Rightarrow 11 x=9$
$\Rightarrow x=\frac{9}{11}$
(ii) $-10=\frac{1+\mathrm{X}}{1-\mathrm{X}}$
$\Rightarrow-10+10 x=1+x$
$\Rightarrow-9 x=-11$
$\Rightarrow x=\frac{11}{9}$
$\rightarrow^{\prime} x^{\prime}$ cannot be more than one, therefore not valid. therefore equation concretion of (D) $=1+x$
$=1+\frac{9}{11}=\frac{20}{11}$
$=1.8181=181.81 \times 10^{-2}$
$\simeq 182 \times 10^{-2}$
