The diameter of a sphere is 6 cm.

Solution:

The diameter of a sphere = 6 cm

Then radius of a sphere $=\frac{6}{2} \mathrm{~cm}=3 \mathrm{~cm}$

The diameter of a wire = 2 mm

Then radius of wire $=1 \mathrm{~mm}=0.1 \mathrm{~cm}$

Now,

Volume of sphere = volume of wire

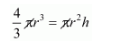
Here,

r = radius

l = length of wire

$\frac{4}{3} \times 3 \times 3 \times 2=0.1 \times 0.1 \times 1$

$36=0.01 l$

$l=\frac{36}{0.01}$

To remove the decimal from base we should multiply both numerator and denumerator by 100,

We get,

$l=3600=36 \mathrm{~m}$

Hence, the correct answer is choice (c).