Question:
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
Solution:
The radius of copper sphere, $R=\frac{18}{2}=9 \mathrm{~cm}$
The volume of sphere $=\frac{4}{3} \pi \times(9)^{3}$
$=\frac{4}{3} \pi \times 729$
$=972 \pi \mathrm{cm}^{2}$
Since,
The sphere is melted and drawn into a long circular wire of length 108 m = 10800 cm
Let r be the radius of wire,
Clearly,
The volume of wire = volume of sphere
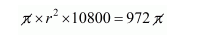
$r^{2}=\frac{972}{10800}$
$=\frac{9}{100}$
$r=\frac{3}{10}$
$r=0.3 \mathrm{~cm}$
And, d = 2r = 0.6 cm
Hence, the diameter of the wire will be equals to $0.6 \mathrm{~cm}$
