The diagonals of a rhombus are 48 cm and 20 cm long.

Diagonals of a rhombus perpendicularly bisect each other. The statement can help us find a side of the rhombus. Consider the following figure.

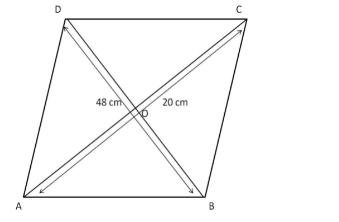
ABCD is the rhombus and AC and BD are the diagonals. The diagonals intersect at point O.

We know:

$\angle D O C=90^{\circ}$

$D O=O B=\frac{1}{2} D B=\frac{1}{2} \times 48=24 \mathrm{~cm}$

Similarly,

$A O=O C=\frac{1}{2} A C=\frac{1}{2} \times 20=10 \mathrm{~cm}$

Using Pythagoras' theorem in the right-angled triangle $\triangle \mathrm{DOC}$, we get:

$D C^{2}=\sqrt{D O^{2}+O C^{2}}$

$=\sqrt{24^{2}+10^{2}}$

$=\sqrt{576+100}$

$=\sqrt{676}$

$=26 \mathrm{~cm}$

DC is a side of the rhombus. 
We know that in a rhombus, all sides are equal.

$\therefore$ Perimeter of $A B C D=26 \times 4=104 \mathrm{~cm}$