The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O such that ∠DAC = 30° and ∠AOB = 70°.
Question:
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O such that ∠DAC = 30° and ∠AOB = 70°. Then, ∠DBC = ?
(a) 40°
(b) 35°
(c) 45°
(d) 50°
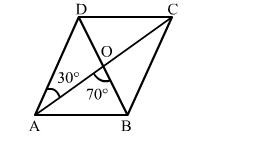
Solution:
(a) 40°
Explanation:
∠OAD = ∠OCB = 30o (Alternate interior angles)
∠AOB + ∠BOC = 180o (Linear pair of angles)
∴ ∠BOC = 180o − 70o = 110o (∠ AOB = 70o)
In ∆BOC, we have:
∠OBC = 180o − (110o + 30o) = 40o
∴ ∠DBC = 40o
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.