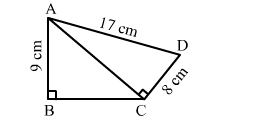
The area of quadrilateral ABCD in the given figure is

(c) $114 \mathrm{~cm}^{2}$

ar (quad. ABCD) =  ar (∆ ABC)  +  ar (∆ ACD)
In right angle triangle ACD, we have:

$A C=\sqrt{\left(17^{2}-8^{2}\right)}=\sqrt{225}=15 \mathrm{~cm}$

In right angle triangle ABC, we have:

$B C=\sqrt{\left(15^{2}-9^{2}\right)}=\sqrt{144}=12 \mathrm{~cm}$

Now, we have the following:

$\operatorname{ar}(\Delta A B C)=\frac{1}{2} \times 12 \times 9=54 \mathrm{~cm}^{2}$

$\operatorname{ar}(\Delta A D C)=\frac{1}{2} \times 15 \times 8=60 \mathrm{~cm}^{2}$

$\operatorname{ar}($ quad $. A B C D)=54+60=114 \mathrm{~cm}^{2}$