The area of an isosceles triangle having

(a) Let $A B C$ be an isosceles triangle in which $A B=A C=4 \mathrm{~cm}$ and $B C=2 \mathrm{~cm}$.

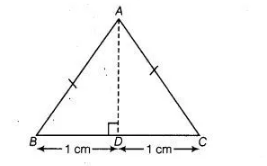
In right angled $\triangle A D B$,

$A B^{2}=A D^{2}+B D^{2}$ [by Pythagoras theorem]

$\Rightarrow \quad(4)^{2}=A D^{2}+1$

$\Rightarrow \quad A D^{2}=16-1$

$\Rightarrow \quad A D^{2}=15$

$\therefore \quad A D=\sqrt{15} \mathrm{~cm}$

[taking positive square root because length is always positive]

$\therefore \quad$ Area of $\triangle A B C=\frac{1}{2} \times B C \times A D \quad\left[\because\right.$ area of triangle $=\frac{1}{2}$ (base $\times$ height $)$ ]

$=\frac{1}{2} \times 2 \times \sqrt{15}=\sqrt{15} \mathrm{~cm}^{2}$

Alternate Method

We know that,

Area of an isosceles triangle $=\frac{a}{4} \sqrt{4 b^{2}-a^{2}}$

where, $b$ is the length of equal sides and $a$ is the length of the base.

Here, the length of side be $b=4 \mathrm{~cm}$ and $a=2 \mathrm{~cm}$

$\therefore$ Area of an isosceles triangle $=\frac{2 \sqrt{4(4)^{2}-4}}{4}=\frac{\sqrt{64-4}}{2}$

$=\frac{\sqrt{60}}{2}=\frac{2 \sqrt{15}}{2}=\sqrt{15} \mathrm{~cm}^{2}$