Question:
The area (in sq. units) of the region bounded by the curves $x^{2}+2 y-1=0, y^{2}+4 x-4=0$ and $y^{2}-4 x-4=0$, in the upper half plane is__________.
Solution:
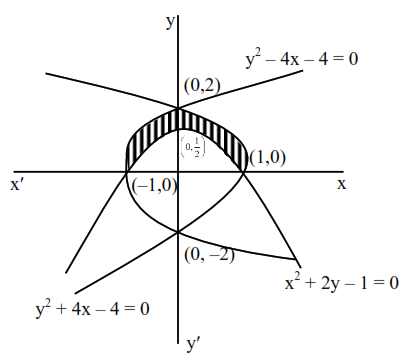
Required Area (shaded)
$=2\left[\int_{0}^{2}\left(\frac{4-y^{2}}{4}\right) d y-\int_{0}^{1}\left(\frac{1-x^{2}}{2}\right) d x\right]$
$=2\left[\frac{4}{3}-\frac{1}{3}\right]=(2)$
