The area (in sq. units) of the region bounded by the curve

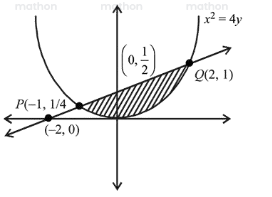
Let points of intersection of the curve and the line be $P$ and $Q$

$x^{2}=4\left(\frac{x+2}{4}\right)$

$x^{2}-x-2=0$

Point are $(2,1)$ and $\left(-1, \frac{1}{4}\right)$

Area $=\int_{-1}^{2}\left[\left(\frac{x+2}{4}\right)-\left(\frac{x^{2}}{4}\right)\right] d x=\left[\frac{x^{2}}{8}+\frac{1}{2} x-\frac{x^{3}}{12}\right]_{-1}^{2}$

$=\left(\frac{1}{2}+1-\frac{2}{3}\right)-\left(\frac{1}{8}-\frac{1}{2}+\frac{1}{12}\right)=\frac{9}{8}$