Question:
The area (in sq. units) of the region bounded by the curves $y=2^{x}$ and $y=|x+1|$, in the first quadrant is:
Correct Option: 1
Solution:
Required Area
$\int_{0}^{1}\left((x+1)-2^{x}\right) d x$
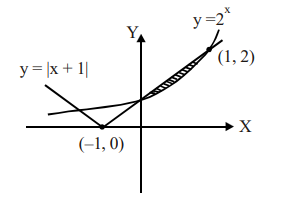
$=\left(\frac{x^{2}}{2}+x-\frac{2^{x}}{\ln 2}\right)_{0}^{1}$
$=\left(\frac{1}{2}+1-\frac{2}{\ln 2}\right)-\left(0+0-\frac{1}{\ln 2}\right)$
$=\frac{3}{2}-\frac{1}{\ln 2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.