The area (in sq. units) in the first quadrant bounded by the parabola

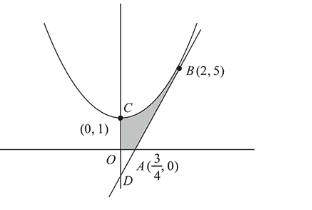
The equation of parabola $x^{2}=y-1$

The equation of tangent at $(2,5)$ to parabola is

$y-5=\left(\frac{d y}{d x}\right)_{(2,5)}(x-2)$

$y-5=4(x-2)$

$4 x-y=3$

Then, the required area

$=\int_{0}^{2}\left\{\left(x^{2}+1\right)-(4 x-3)\right\} d x$-Area of $\triangle A O D$

$=\int_{0}^{2}\left(x^{2}-4 x+4\right) d x-\frac{1}{2} \times \frac{3}{4} \times 3$

$=\left[\frac{(x-2)^{3}}{3}\right]_{0}^{2}-\frac{9}{8}=\frac{37}{24}$