Question:
The area (in sq. units) bounded by the parabola $y=x^{2}-1$, the tangent at the point $(2,3)$ to it and the $y$-axis is :
Correct Option: , 3
Solution:
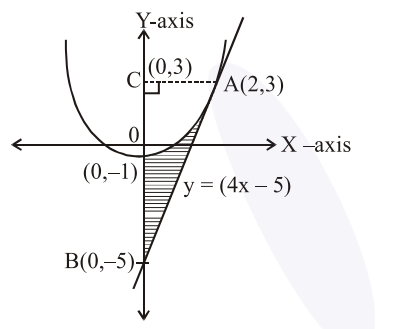
Equation of tangent at $(2,3)$ on
$y=x^{2}-1$, is $y=(4 x-5)$ ............(i)
$\therefore$ Required shaded area
$=\operatorname{ar}(\Delta \mathrm{ABC})-\int_{-1}^{3} \sqrt{\mathrm{y}+1} \mathrm{dy}$
$=\frac{1}{2} \cdot(8) \cdot(2)-\frac{2}{3}\left((y+1)^{3 / 2}\right)_{-1}^{3}$
$=8-\frac{16}{3}=\frac{8}{3}$ (square units)
