Question:
The area bounded by the curve $y=x|x|, x$-axis and the ordinates $x=-1$ and $x=1$ is given by
[Hint: $y=x^{2}$ if $x>0$ and $y=-x^{2}$ if $x<0$ ]
A. 0
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{4}{3}$
Solution:
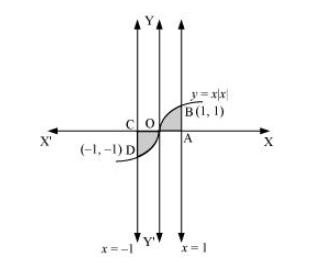
Required area $=\int_{-1}^{1} y d x$
$=\int_{-1}^{1} x|x| d x$
$=\int_{-1}^{0} x^{2} d x+\int_{0}^{1} x^{2} d x$
$=\left[\frac{x^{3}}{3}\right]_{-1}^{0}+\left[\frac{x^{3}}{3}\right]_{0}^{1}$
$=-\left(-\frac{1}{3}\right)+\frac{1}{3}$
$=\frac{2}{3}$ units
Thus, the correct answer is C.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.