Question:
The angular momentum of a planet of mass $M$ moving around the sun in an elliptical orbit is $\overrightarrow{\mathrm{L}}$. The magnitude of the areal velocity of the planet is:
Correct Option: , 4
Solution:
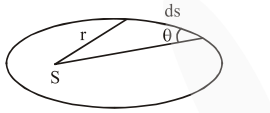
For small displacement ds of the planet its area can be written as
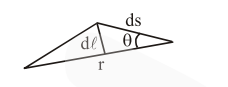
$\mathrm{dA}=\frac{1}{2} \mathrm{rd} \ell$
$=\frac{1}{2} \mathrm{rds} \sin \theta$
A. vel $=\frac{\mathrm{dA}}{\mathrm{dt}}=\frac{1}{2} \mathrm{r} \sin \theta \frac{\mathrm{ds}}{\mathrm{dt}}=\frac{\mathrm{Vr} \sin \theta}{2}$
$\frac{\mathrm{dA}}{\mathrm{dt}}=\frac{1}{2} \frac{\mathrm{mVr} \sin \theta}{\mathrm{m}}=\frac{\mathrm{L}}{2 \mathrm{~m}}$
