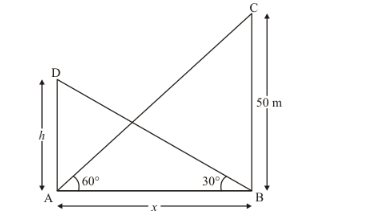
The angle of elevation of the top of the building from the foot of the tower is 30°

Let AD be the building of height h m. and an angle of elevation of top of building from the foot of tower is 30° and an angle of the top of tower from the foot of building is 60°.

Let AD = h, AB = x and BC = 50 and , 

So we use trigonometric ratios.

In a triangle,

$\Rightarrow \quad \tan 60^{\circ}=\frac{50}{x}$

$\Rightarrow \quad \sqrt{3}=\frac{50}{x}$

$\Rightarrow \quad x=\frac{50}{\sqrt{3}}$

Again in a triangle,

$\Rightarrow \quad \tan 30^{\circ}=\frac{A D}{A B}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{x}$

$\Rightarrow \quad h=\frac{x}{\sqrt{3}}$

$\Rightarrow \quad h=\frac{50}{\sqrt{3} \times \sqrt{3}}$

$\Rightarrow \quad h=\frac{50}{3}$

Hence the height of building is $\frac{50}{3} \mathrm{~m}$.