The angle of elevation of the top of a tower from a point on the same level as the foot of the tower is 30°

Let $A B$ be the tower.

We have:

$C D=150 \mathrm{~m} . \angle A C B=30^{\circ}$ and $\angle A D B=60^{\circ}$

Let:

$A B=h \mathrm{~m}$ and $B D=x \mathrm{~m}$

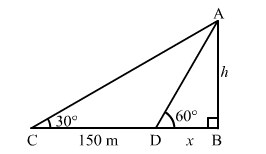
In the right $\triangle A B D$, we have:

$\frac{A B}{A D}=\tan 60^{\circ}=\sqrt{3}$

$\Rightarrow \frac{h}{x}=\sqrt{3}$

$\Rightarrow x=\frac{h}{\sqrt{3}}$

Now, in the right $\Delta A C B$, we have:

$\frac{A B}{B C}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}$

$\Rightarrow \frac{h}{x+150}=\frac{1}{\sqrt{3}}$

$\Rightarrow \sqrt{3} h=x+150$

On putting $x=\frac{h}{\sqrt{3}}$ in the above equation, we get:

$\sqrt{3} h=\frac{h}{\sqrt{3}}+150$

$\Rightarrow 3 h=h+150 \sqrt{3}$

$\Rightarrow 2 h=150 \sqrt{3}$

$\Rightarrow h=\frac{150 \sqrt{3}}{2}=75 \sqrt{3}=75 \times 1.732=129.9 \mathrm{~m}$

Hence, the height of the tower is 129.9 m.