The angle of elevation of the top of a tower from a point on the ground 30 m away from the foot of the tower is 30°.

(b) $10 \sqrt{3} \mathrm{~m}$

Let $A B$ be the tower and $O$ be the point of observation.

Also,

$\angle A O B=30^{\circ}$ and $O B=30 \mathrm{~m}$

Let:

$A B=h \mathrm{~m}$

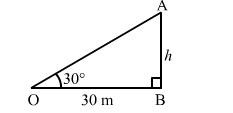
In $\triangle A O B$, we have:

$\frac{A B}{O B}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}$

$\Rightarrow \frac{h}{30}=\frac{1}{\sqrt{3}}$

$\Rightarrow h=\frac{30}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{30 \sqrt{3}}{3}=10 \sqrt{3} \mathrm{~m}$

Hence, the height of the tower is $10 \sqrt{3} \mathrm{~m}$.