The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°.

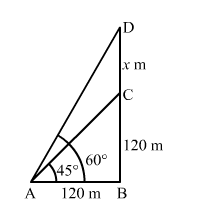
Let BC and CD be the heights of the tower and the flagstaff, respectively.

We have,

$\mathrm{AB}=120 \mathrm{~m}, \angle \mathrm{BAC}=45^{\circ}, \angle \mathrm{BAD}=60^{\circ}$

Let $\mathrm{CD}=x$

In $\Delta \mathrm{ABC}$,

$\tan 45^{\circ}=\frac{\mathrm{BC}}{\mathrm{AB}}$

$\Rightarrow 1=\frac{\mathrm{BC}}{120}$

$\Rightarrow \mathrm{BC}=120 \mathrm{~m}$

Now, in $\triangle \mathrm{ABD}$,

$\tan 60^{\circ}=\frac{\mathrm{BD}}{\mathrm{AB}}$

$\Rightarrow \sqrt{3}=\frac{\mathrm{BC}+\mathrm{CD}}{120}$

$\Rightarrow \mathrm{BC}+\mathrm{CD}=120 \sqrt{3}$

$\Rightarrow 120+x=120 \sqrt{3}$

$\Rightarrow x=120 \sqrt{3}-120$

$\Rightarrow x=120(\sqrt{3}-1)$

$\Rightarrow x=120(1.732-1)$

$\Rightarrow x=120(0.732)$

$\Rightarrow x=87.84 \approx 87.8 \mathrm{~m}$

So, the height of the flagstaff is 87.8 m.