The angle of elevation of the top of a tower

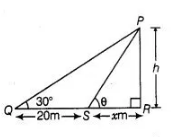
Let the height of the tower be $h$.

also, $\quad S R=x \mathrm{~m}, \angle P S R=\theta$

Given that, $Q S=20 \mathrm{~m}$

and $\angle P Q R=30^{\circ}$

Now, in $\triangle P S R$,

$\tan \theta=\frac{P R}{S R}=\frac{h}{x}$

$\Rightarrow$ $\tan \theta=\frac{h}{x}$

$\Rightarrow$ $x=\frac{h}{\tan \theta}$  $\ldots$ (i)

Now, in $\triangle P Q R$, 

$\tan 30^{\circ}=\frac{P R}{Q R}=\frac{P R}{Q S+S R}$

$\Rightarrow$ $\tan 30^{\circ}=\frac{h}{20+x}$

$\Rightarrow$ $20+x=\frac{h}{\tan 30^{\circ}}=\frac{h}{1 / \sqrt{3}}$

$\Rightarrow$ $20+x=h \sqrt{3}$

$\Rightarrow$ $20+\frac{h}{\tan \theta}=h \sqrt{3}$ .....(ii) [from Eq. (i)]

Since, after moving $20 \mathrm{~m}$ towards the tower the angle of elevation of the top increases by $15^{\circ}$.

i.e. $\angle P S R=\theta=\angle P Q R+15^{\circ}$

$\Rightarrow \quad \theta=30^{\circ}+15=45^{\circ}$

$\therefore \quad 20+\frac{h}{\tan 45^{\circ}}=h \sqrt{3}$ [from Eq. (i)]

$\Rightarrow \quad 20+\frac{h}{1}=h \sqrt{3}$

$\Rightarrow \quad h(\sqrt{3}-1)=20$

$\therefore$ $h=\frac{20}{\sqrt{3}-1} \cdot \frac{\sqrt{3}+1}{\sqrt{3}+1}$ [by rationalisation]

$\Rightarrow$ $=\frac{20(\sqrt{3}+1)}{3-1}=\frac{20(\sqrt{3}+1)}{2}$

$\Rightarrow$ $=10(\sqrt{3}+1) m$

Hence, the required height of tower is $10(\sqrt{3}+1) \mathrm{m}$.