The angle of elevation of the top of a chimney from the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°.

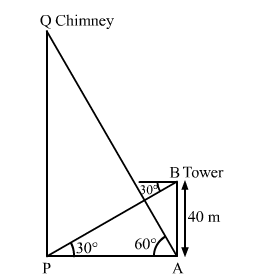
Let PQ be the chimney and AB be the tower.

We have,

$\mathrm{AB}=40 \mathrm{~m}, \angle \mathrm{APB}=30^{\circ}$ and $\angle \mathrm{PAQ}=60^{\circ}$

In $\Delta \mathrm{ABP}$

$\tan 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{AP}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{40}{\mathrm{AP}}$

$\Rightarrow \mathrm{AP}=40 \sqrt{3} \mathrm{~m}$

Now, in $\Delta \mathrm{APQ}$,

$\tan 60^{\circ}=\frac{\mathrm{PQ}}{\mathrm{AP}}$

$\Rightarrow \sqrt{3}=\frac{\mathrm{PQ}}{40 \sqrt{3}}$

$\therefore \mathrm{PQ}=120 \mathrm{~m}$

So, the height of the chimney is 120 m.

Hence, the height of the chimney meets the pollution norms.

In this question, management of air pollution has been shown.
a