The angle of elevation of a stationery cloud from a point 2500 m above a lake is 15°

Let AB be the surface of lake and P be the point of observation such that m. Let C be the position of cloud and  be the reflection in the lake. Then

Let  be the perpendicular from P on CB.

Let $\mathrm{PQ}=x \mathrm{~m}, \mathrm{CQ}=h, \mathrm{QB}=2500 \mathrm{~m}$. then $\mathrm{CB}=h+2500$ consequently $\mathrm{C}^{\prime} \mathrm{B}=h+2500 \mathrm{~m} .$ and $\angle \mathrm{CPQ}=15^{\circ}, \angle Q P C^{\prime}=45^{\circ}$.

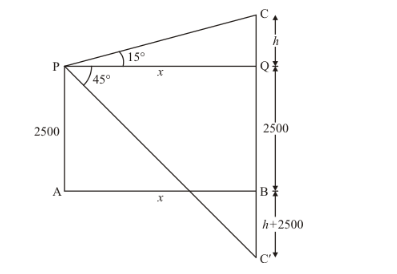
Here we have to find height of cloud.

We use trigonometric ratios.

$\ln \triangle P C Q$

$\Rightarrow \tan 15^{\circ}=\frac{C Q}{P Q}$

$\Rightarrow 2-\sqrt{3}=\frac{h}{x}$

$\Rightarrow x=\frac{h}{2-\sqrt{3}}$

Again in $_{\Delta} P Q C^{\prime}$,

$\Rightarrow \tan 45^{\prime}=\frac{Q B+B C^{\prime}}{P Q}$

$\Rightarrow \mathrm{I}=\frac{2500+h+2500}{x}$

$\Rightarrow x=5000+h$

$\Rightarrow \frac{h}{2-\sqrt{3}}=5000+h$

$\Rightarrow h=2500(\sqrt{3}-1)$

$\Rightarrow C B=2500+2500(\sqrt{3}-1)$

$\Rightarrow C B=2500 \sqrt{3}$

Hence the height of cloud is $2500 \sqrt{3} \mathrm{~m}$.