The angle of depression from the top of a tower of a point A on the ground is 30°.

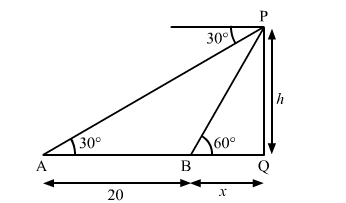
Let PQ be the tower.

We have,

$\mathrm{AB}=20 \mathrm{~m}, \angle \mathrm{PAQ}=30^{\circ}$ and $\angle \mathrm{PBQ}=60^{\circ}$

Let $\mathrm{BQ}=x$ and $\mathrm{PQ}=h$

In $\Delta \mathrm{PBQ}$,

$\tan 60^{\circ}=\frac{\mathrm{PQ}}{\mathrm{BQ}}$

$\Rightarrow \sqrt{3}=\frac{h}{x}$

$\Rightarrow h=x \sqrt{3} \quad \ldots \ldots$ (i)

Also, in $\triangle \mathrm{APQ}$

$\tan 30^{\circ}=\frac{\mathrm{PQ}}{\mathrm{AQ}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{\mathrm{AB}+\mathrm{BQ}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{x \sqrt{3}}{20+x} \quad[$ Using (i) $]$

$\Rightarrow 20+x=3 x$

$\Rightarrow 3 x-x=20$

$\Rightarrow 2 x=20$

$\Rightarrow x=\frac{20}{2}$

$\Rightarrow x=10 \mathrm{~m}$

From (i),

$h=10 \sqrt{3}=10 \times 1.732=17.32 \mathrm{~m}$

Also, $\mathrm{AQ}=\mathrm{AB}+\mathrm{BQ}=20+10=30 \mathrm{~m}$

So, the height of the tower is 17.32 m and its distance from the point A is 30 m.