The angle between two altitudes

Let the parallelogram be ABCD, in which ∠ADC and ∠ABC are obtuse angles. Now, DE and DF are two altitudes of parallelogram and angle between them is 60°.

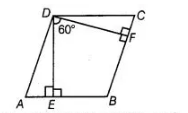
Now, $B E D F$ is a quadrilateral, in which $\angle B E D=\angle B F D=90^{\circ}$

$\therefore$  $\angle F B E=360^{\circ}-(\angle F D E+\angle B E D+\angle B F D)$

$=360^{\circ}-\left(60^{\circ}+90^{\circ}+90^{\circ}\right)$

$=360^{\circ}-240^{\circ}=120^{\circ}$

Since, $A B C D$ is a parallelogram.

$\therefore$ $\angle A D C=120^{\circ}$

Now, $\angle A+\angle B=180^{\circ}$ [sum of two cointerior angles is $180^{\circ}$ ]

$5=180^{\circ}-120^{\circ}$ $[\because \angle F B E=\angle B]$

$\Rightarrow$ $\angle A=60^{\circ}$ 

Also,  $\angle C=\angle A=60^{\circ}$

Hence, angles of the parallelogram are $60^{\circ}, 120^{\circ}, 60^{\circ}$ and $120^{\circ}$, respectively.