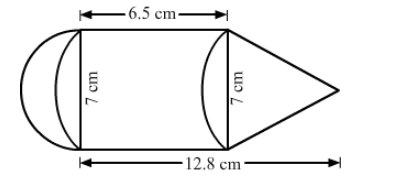
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other.

Diameter of the cylindrical part =7 cm
Therefore,radius of the cylindrical part = 3.5 cm

Volume of hemisphere $=\frac{2}{3} \pi \mathrm{r}^{3}=\frac{2}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 3.5=89.83 \mathrm{~cm}^{3}$

Volume of the cylinder $=\pi r^{2} \mathrm{~h}=\frac{22}{7} \times 3.5 \times 3.5 \times 6.5=250.25 \mathrm{~cm}^{3}$

Height of cone $=12.8-6.5=6.3 \mathrm{~cm}$

Volume of the cone $=\frac{1}{3} \pi \mathrm{r}^{2} h=\frac{1}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 6.3=80.85 \mathrm{~cm}^{3}$

Total volume $=89.83+250.25+80.85=420.93 \mathrm{~cm}^{3}$