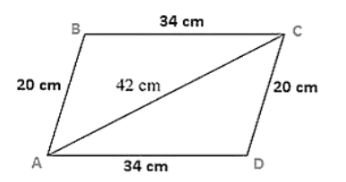
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal

The adjacent sides of a parallelogram ABCD measures 34 cm and 20 cm, and the diagonal AC measures 42 cm.

Area of the parallelogram = Area of triangle ADC + Area of triangle ABC

Note: Diagonal of a parallelogram divides into two congruent triangles

Therefore,

Area of the parallelogram = 2 × (Area of triangle ABC)

Now, for area of triangle ABC

Perimeter = 2s = AB + BC + CA

2s = 34 cm + 20 cm + 42 cm

s = 48 cm

By using Heron's Formula

Area of the triangle $\mathrm{ABC}=\sqrt{\mathrm{s} \times(\mathrm{s}-\mathrm{a}) \times(\mathrm{s}-\mathrm{b}) \times(\mathrm{s}-\mathrm{c})}$

$=\sqrt{48 \times(14) \times(28) \times(6)}$

$=336 \mathrm{~cm}^{2}$

Therefore, area of parallelogram ABCD = 2 × (Area of triangle ABC)

Area of parallelogram $=2 \times 336 \mathrm{~cm}^{2}$

Area of parallelogram $A B C D=672 \mathrm{~cm}^{2}$