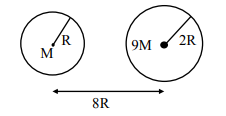
Suppose two planets (spherical in shape) of radii R and 2R, but mass M and 9 M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the
surface of the second planet is $\sqrt{\frac{a}{7} \frac{G M}{R}}$ then the
value of 'a' is ________.
[Given : The two planets are fixed in their position]

Acceleration due to gravity will be zero at P therefore,
$\frac{\mathrm{GM}}{\mathrm{x}^{2}}=\frac{\mathrm{G} 9 \mathrm{M}}{(8 \mathrm{R}-\mathrm{x})^{2}}$
$8 R-x=3 x$
$\mathrm{x}=2 \mathrm{R}$
Apply conservation of energy and consider velocity at P is zero.
$\frac{1}{2} \mathrm{mv}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}-\frac{\mathrm{G} 9 \mathrm{Mm}}{7 \mathrm{R}}=0-\frac{\mathrm{GMm}}{2 \mathrm{R}}-\frac{\mathrm{G} 9 \mathrm{Mm}}{6 \mathrm{R}}$
$\therefore \mathrm{V}=\sqrt{\frac{4}{7} \frac{\mathrm{GM}}{\mathrm{R}}}$
