Sucrose hydrolyses in acid solution into glucose and fructose following first order rate law with a half-life of $3.33 \mathrm{~h}$ at $25^{\circ} \mathrm{C}$. After $9 \mathrm{~h}$, the fraction of sucrose remaining is $f$. The value of $\log _{10}\left(\frac{1}{f}\right)$ is $\times 10^{-2}$. (Rounded off to the nearest integer)
[Assume : $\ln 10=2.303, \ln 2=0.693$ ]
Given :
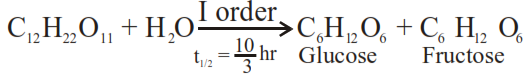
$\mathrm{t}=0 \quad \mathrm{a}=[\mathrm{A}]_{0}$
$\mathrm{t}=9 \mathrm{hr} \quad \mathrm{a}-\mathrm{X}=[\mathrm{A}]_{\mathrm{t}}$
from I order kinetic $: \frac{\mathrm{k} \times \mathrm{t}}{2.303}=\log \frac{|\mathrm{A}|_{0}}{|\mathrm{~A}|_{\mathrm{t}}}$
$\Rightarrow \frac{\ln 2 \times 9}{\frac{10}{3} \times 2.303}=\log \left(\frac{1}{f}\right)$
$\Rightarrow \frac{0.693 \times 9 \times 3}{23.03}=\log \left(\frac{1}{f}\right)$
$\Rightarrow \log \left(\frac{1}{f}\right)=0.81246=81.24 \times 10^{-2}$
$\Rightarrow x=81$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.