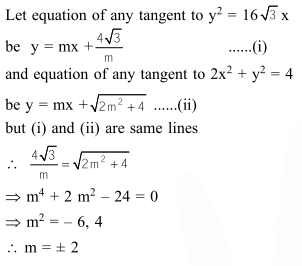Statement–1 : An equation of a common tangent

Statement-1 : An equation of a common tangent to the parabola $y^{2}=16 \sqrt{3} x$ and the ellipse $2 x^{2}+y^{2}=4$ is $y=2 x+2 \sqrt{3}$

Statement-2 : If the line $y=m x+\frac{4 \sqrt{3}}{m},(m \neq 0)$ is a common tangent to the parabola $y^{2}$ $16 \sqrt{3} \mathrm{x}$ and the ellipse $2 \mathrm{x}^{2}+\mathrm{y}^{2}=4$, then $\mathrm{m}$ satisfies $\mathrm{m}^{4}+2 \mathrm{~m}^{2}=24$