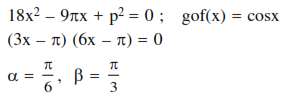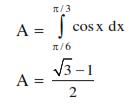Question:
Let $g(x)=\cos x^{2}, f(x)=\sqrt{x}$ and $\alpha, \beta(\alpha<\beta)$ be the roots of the quadratic equation $18 x^{2}-9 \pi x+\pi^{2}=0$. Then the area (in sq. units) bounded by the curve $y=(g o f)(x)$ and the lines $x=\alpha, x=\beta$ and $y=0$ is-
Correct Option: , 4
Solution: