Question:
Let the mean and variance of the frequency distribution
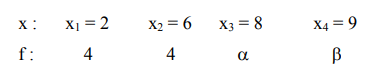
be 6 and $6.8$ respectively. If $x_{3}$ is changed from 8 to 7 , then the mean for the new data will be:
Correct Option: , 3
Solution:
Given $32+8 \alpha+9 \beta=(8+\alpha+\beta) \times 6$
$\Rightarrow 2 \alpha+3 \beta=16$ .............(I)
Also, $4 \times 16+4 \times \alpha+9 \beta=(8+\alpha+\beta) \times 6.8$
$\Rightarrow 640+40 \alpha+90 \beta=544+68 \alpha+68 \beta$
$\Rightarrow 28 \alpha-22 \beta=96$
$\Rightarrow 14 \alpha-11 \beta=48$ ........................(II)
from (i) \& (ii)
$\alpha=5 \& \beta=2$
so, new mean $=\frac{32+35+18}{15}=\frac{85}{15}=\frac{17}{3}$
