Let
$A=\left\{(x, y) \in \mathbf{R} \times \mathbf{R} \mid 2 x^{2}+2 y^{2}-2 x-2 y=1\right\}$
$B=\left\{(x, y) \in \mathbf{R} \times \mathbf{R} \mid 4 x^{2}+4 y^{2}-16 y+7=0\right\}$ and
$C=\left\{(x, y) \in \mathbf{R} \times \mathbf{R} \mid x^{2}+y^{2}-4 x-2 y+5 \leq r^{2}\right\}$
Then the minimum value of $|\mathrm{r}|$ such that
$\mathrm{A} \cup \mathrm{B} \subseteq \mathrm{C}$ is equal to
Correct Option: , 3
$\mathrm{S}_{1}: \mathrm{x}^{2}+\mathrm{y}^{2}-\mathrm{x}-\mathrm{y}-\frac{1}{2}=0 ; \mathrm{C}_{1}\left(\frac{1}{2}, \frac{1}{2}\right)$
$r_{1}=\sqrt{\frac{1}{4}+\frac{1}{4}+\frac{1}{2}}=1$
$\mathrm{S}_{2}: \mathrm{x}^{2}+\mathrm{y}^{2}-4 \mathrm{y}+\frac{7}{4}=0 ; \mathrm{C}_{2}:(0,2)$
$r_{2}=\sqrt{4-\frac{7}{4}}=\frac{3}{2}$
$S_{3}: x^{2}+y^{2}-4 x-2 y+5-r^{2}=0$
$\mathrm{C}_{3}:(2,1)$
$r_{3}=\sqrt{4+1-5+r^{2}}=|r|$
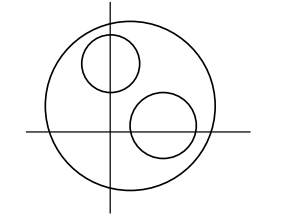
$C_{1} C_{3}=\sqrt{\frac{5}{2}}$
$\left.\sqrt{\frac{5}{2}} \leq|\mathrm{r}-1| \Rightarrow \begin{array}{rl}\mathrm{r} & \leq 1+\sqrt{\frac{5}{2}} \\ \mathrm{r} & \geq \frac{3}{2}+\sqrt{5}\end{array}\right\}$
$\mathrm{C}_{2} \mathrm{C}_{3}=\sqrt{5} \leq\left|\mathrm{r}-\frac{3}{2}\right|$
$\left.\begin{array}{l}r-\frac{3}{2} \geq \sqrt{5} \\ r-\frac{3}{2} \leq-\sqrt{5}\end{array}\right\}$
