Question:
The length of the chord of the parabola $x^{2}=4 y$
having equation $x-\sqrt{2} y+4 \sqrt{2}=0$ is :
Correct Option: , 3
Solution:
$x^{2}=4 y$
$x-\sqrt{2} y+4 \sqrt{2}=0$
Solving together we get
$x^{2}=4\left(\frac{x+4 \sqrt{2}}{\sqrt{2}}\right)$
$\sqrt{2} x^{2}+4 x+16 \sqrt{2}$
$\sqrt{2} x^{2}-4 x-16 \sqrt{2}=0$
$\mathrm{x}_{1}+\mathrm{x}_{2}=2 \sqrt{2} ; \quad \mathrm{x}_{1} \mathrm{x}_{2}=\frac{-16 \sqrt{2}}{\sqrt{2}}=-16$
Similarly,
$(\sqrt{2} y-4 \sqrt{2})^{2}=4 y$
$2 y^{2}+32-16 y=4 y$
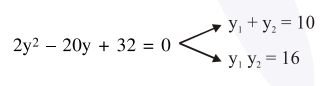
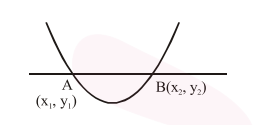
$\ell_{\mathrm{AB}}=\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}$
$=\sqrt{(2 \sqrt{2})^{2}+64+(10)^{2}-4(16)}$
$=\sqrt{8+64+100-64}$
$=\sqrt{108}=6 \sqrt{3}$
Option (3)
