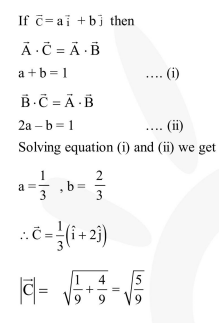Solve this following

Let $\overrightarrow{\mathrm{A}}=(\hat{\mathrm{i}}+\hat{\mathrm{j}})$ and $\overrightarrow{\mathrm{B}}=(2 \hat{\mathrm{i}}-\hat{\mathrm{j}})$. The magnitude of a coplanar vector $\overrightarrow{\mathrm{C}}$ such that $\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}$,

is given by :-