Question:
Let $I=\int_{a}^{b}\left(x^{4}-2 x^{2}\right) d x$. If I is minimum then
the ordered pair (a, b) is :
Correct Option: , 2
Solution:
Let $f(x)=x^{2}\left(x^{2}-2\right)$
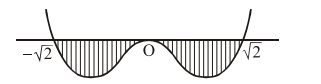
As long as $f(x)$ lie below the $x$-axis, definite integral will remain negative,
so correct value of $(a, b)$ is $(-\sqrt{2}, \sqrt{2})$ for minimum of I
